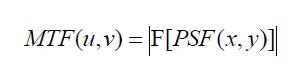Como hemos dicho, la resolución espacial es una medida de la calidad de imagen, ya que describe la habilidad de un sistema para captar con exactitud los objetos en las dos dimensiones espaciales de la imagen. De manera intuitiva se puede definir como la habilidad del sistema para distinguir dos objetos como separados a medida que se hacen más pequeños y cercanos. Cuando la resolución espacial no es la adecuada, la imagen manifiesta borrosidad (blurring), como se observa en la Figura 1.
Figura 1. Imagen con (a) alta y (b) baja resolución espacial.
¿Cómo se mide la resolución espacial?
Una forma de determinar la resolución espacial de un sistema de imagen es mediante la función de respuesta a un impulso (point spread function, PSF). La PSF se obtiene como la imagen de una fuente puntual, como se ilustra en la Figura 2. Si la fuente puntual se coloca en diferentes posiciones del receptor de imagen del sistema y se obtiene la misma PSF, se dice que el sistema es estacionario o invariante en el espacio. Una vez determinada la PSF se puede obtener un perfil de la imagen (es decir, una gráfica cuyo eje Y representa el nivel de gris o valor de píxel y el eje X representa la posición o distancia). La resolución espacial (en unidades de longitud) se determina midiendo directamente el FWHM del perfil (full width at half maximum, es el ancho del perfil medido justamente a la mitad de la altura del punto máximo).
Figura 2. La PSF es la imagen de un objeto o fuente puntual.
Una descripción más precisa de la resolución del sistema de imagen la proporciona la función de transferencia de modulación (modulation transfer function, MTF). La MTF relaciona la pérdida de contraste en la imagen con la frecuencia espacial, es decir, a partir de ella puede estimarse el tamaño mínimo (i.e. resolución espacial) de los objetos que pueden distinguirse con un contraste aceptable en la imagen. La MTF se obtiene mediante el módulo de la transformada de Fourier de la PSF:
y la función se normaliza dividiéndola entre el valor de MTF(0,0), esto significa que la MTF vale 1 a la frecuencia cero. Nótese que la ecuación anterior es bidimensional (u y v representan la frecuencia espacial en el eje horizontal y vertical, respectivamente) ya que partimos de una PSF tridimensional (distribuida en una imagen: coordenadas de posición X y Y, valor de píxel en Z).
¿Cómo se interpreta la MTF?
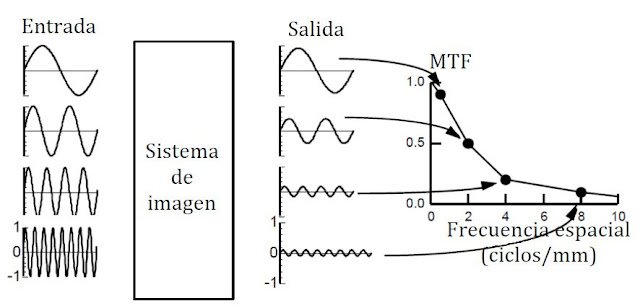
Supongamos que conseguimos nuestra fuente puntual, obtuvimos una imagen de ella que representa la PSF, aplicamos la ecuación para obtener la MTF y normalizamos... ahora, ¿qué significa? ¿Dónde aparece la resolución espacial? Para responder a estas preguntas miremos la Figura 3, que muestra un esquema conceptual de la MTF. Las señales de entrada al sistema están representadas por funciones senoidales de diferentes frecuencias. Después se pasar por el sistema de imagen, las señales de salida tienen una menor amplitud que las señales originales (de entrada), pero conservan su frecuencia. Notamos que una mayor frecuencia en la señal de entrada implica una menor amplitud en la señal de salida. Es decir, la amplitud de la salida se ve afectada por el sistema de imagen y este efecto es función de la frecuencia espacial. La MTF del esquema de la Figura 3 relaciona frecuencia espacial de entrada (eje X) y amplitud de la salida (eje Y), la gráfica indica que para frecuencias espaciales pequeñas (correspondientes a objetos grandes), la señal se transfiere casi completamente (no hay gran pérdida en contraste en la imagen de salida). A medida que la frecuencia espacial aumenta (objetos más pequeños), la amplitud de la señal de salida (y por tanto, el contraste) disminuye.
Figura 3. La MTF describe cómo el sistema afecta el detalle en una imagen.
Un criterio para determinar la resolución espacial de un sistema a partir de la MTF consiste en medir la MTF del sistema y luego distinguir en la gráfica a qué valor de frecuencia espacial (unidades = inverso de la longitud, ciclos/mm, etc.) corresponde un 0.1 de la MTF. Para transformar ese dato a unidades de longitud se usa el criterio de Nyquist, realizando la siguiente operación: Resolución espacial (longitud) = 1/(2*Frecuencia espacial). Para un sistema ideal que no modificadara la información de entrada, la MTF valdría 1 para todas las frecuencias espaciales; para detectores no ideales la MTF va disminuyendo a medida que aumenta la frecuencia espacial, es decir, se tiene menor contraste en la imagen a medida que disminuye el tamaño de los objetos de entrada. Mientras más cercano a 1 sea el valor de la MTF a altas frecuencias, mejor será la resolución espacial del sistema.
Métodos alternativos a la fuente puntual (PSF)
Ahora bien, la MTF sigue dependiendo de que conozcamos previamente la PSF del sistema y ésta es difícil de determinar ya que se requiere una fuente puntual infinitesimal. Una fuente puntual es una idealización de las fuentes de fotones (como la de rayos X, por ejemplo), que no son nada puntuales. Además, si conociéramos la PSF podríamos determinar la resolución espacial con el FWHM directamente. Esta dificultad puede resolverse empleando una fuente lineal cuya imagen da lugar a la función de respuesta a una línea (line spread function, LSF), mostrada en la Figura 4. La relación entre la PSF y la LSF es que, para sistemas invariantes en el espacio e invariantes ante rotaciones, ésta es una representación unidimensional de la PSF tridimensional (equivalente al perfil que trazamos a la PSF para determinar el FWHM). De este modo, la MTF unidimensional puede obtenerse a partir del módulo de la transformada de Fourier de la LSF unidimensional:
Figura 4. La LSF es la imagen de un objeto o fuente lineal.
La LSF de un sistema de imagen se puede obtener empleando una rendija muy delgada y opaca. La dificultad que este método implica es que el uso de rendijas requiere de fabricación y alineamiento precisos, una alta exposición de la radiación para permitir la transmisión a través de la rendija y una corrección por el tamaño finito del grosor de la rendija. Esto se soluciona empleando únicamente la mitad de la rendija, es decir, una placa opaca con un borde pulido. La imagen que se obtiene representa la función de respuesta a un borde (edge spread function, ESF) y se muestra en la Figura 5. Matemáticamente, la LSF se obtiene derivando la ESF y por lo tanto puede emplearse ésta para determinar la resolución espacial de un sistema de imagen mediante la MTF:
Figura 5. La ESF es la imagen de un objeto opaco con un borde.
Se han empleado diversos métodos analíticos y experimentales para obtener la MTF a partir de la LSF y la ESF. Fujita et al. diseñaron el método de sobremuestreo aplicado a la LSF, Samei et al. retomaron el sobremuestro pero combinándolo con otras técnicas de procesamiento de imagen, usando la ESF. Actualmente el método de la ESF, o método de borde, es el que más se emplea por su simplicidad y practicidad.
Referencias: el handbook, el Bushberg y artículos útiles
2. Cunningham IA. “Applied Linear-Systems Theory”, in Handbook of Medical Imaging, Vol. 1, Physics and Psychophysics, edited by J Beutel, HL Kundel and RL Van Metter, Bellingham, WA. SPIE Press, 2000; 79-159.
3. Fujita H, Tsai DY, Itoh T, et al. A Simple Method for Determining the Modulation Transfer Function in Digital Radiography. Med. Phys., 1992; 11: 34-39.
4. Samei E, Flynn MJ, Reimann DA. A Method for Measuring the Presampled MTF of Digital Radiographic Systems Using an Edge Test Device. Med. Phys., 1998; 25: 102-113.